Intervalos Musicales: Los Elementos Fundamentales de la Música
Resumen:
Los intervalos musicales son las distancias en altura entre dos notas, sirviendo como elemento fundamental sobre el cual se construyen la melodía, la armonía y las escalas. Un sólido entendimiento de los intervalos es crucial para cualquier músico, pues constituyen el vocabulario básico de la música. Este artículo profundiza en su definición, clasificación y aplicación, proporcionando ejemplos claros y consejos prácticos para reconocerlos auditivamente.
Palabras clave:
Intervalos musicales, tonos, semitonos, consonancia, disonancia, melodía, armonía, entrenamiento auditivo, teoría musical, escalas, acordes.
Introducción: ¿Qué es un intervalo musical?
Imagina que la música es un idioma. Si las notas son las letras, entonces los intervalos son las sílabas: los sonidos esenciales que se combinan para formar palabras (acordes) y oraciones (melodías). Un intervalo es simplemente la distancia entre dos alturas. Esta distancia puede escucharse cuando las notas se tocan una tras otra (intervalo melódico) o simultáneamente (intervalo armónico).
Dominar los intervalos transforma tu relación con la música. Te permite identificar acordes y melodías de oído, improvisar con confianza y comprender la estructura de cualquier composición. Es la llave que abre la puerta de simplemente tocar notas a entender verdaderamente la música que creas y escuchas.
Cómo definir y clasificar intervalos
Cada intervalo tiene dos partes en su nombre: un número (o distancia) y una cualidad (o carácter).
1. Número del intervalo (Distancia):
El número se encuentra contando los nombres de las notas desde la primera hasta la segunda, incluyendo ambas. Por ejemplo, la distancia de Do a Sol es una quinta porque abarca cinco nombres: Do, Re, Mi, Fa, Sol.
- Unísono: 1 nombre de nota (Do-Do)
- Segunda: 2 nombres de nota (Do-Re)
- Tercera: 3 nombres de nota (Do-Mi)
- Cuarta: 4 nombres de nota (Do-Fa)
- Quinta: 5 nombres de nota (Do-Sol)
- Sexta: 6 nombres de nota (Do-La)
- Séptima: 7 nombres de nota (Do-Si)
- Octava: 8 nombres de nota (Do-Do)
2. Cualidad del intervalo (Carácter):
La cualidad describe el sonido y tamaño preciso del intervalo, medido en semitonos (el paso más pequeño en la música occidental, como de una tecla de piano a la siguiente). Las cualidades se dividen en dos familias principales:
- Justos: Los unísonos, cuartas, quintas y octavas se llaman 'Justos'. Tienen un sonido puro y estable.
- Mayores y Menores: Las segundas, terceras, sextas y séptimas pueden ser 'Mayores' (más grandes) o 'Menores' (más pequeñas). Los intervalos mayores suelen sonar brillantes y alegres, mientras que los menores pueden sonar más apagados o melancólicos.
Además, cualquier intervalo puede hacerse un semitono más grande (Aumentado) o un semitono más pequeño (Disminuido), lo que añade tensión y color.
3. Efecto acústico (Consonancia vs. Disonancia):
Los intervalos también pueden describirse por su sonido:
- Consonantes: Intervalos que suenan estables y en reposo. Incluyen los intervalos justos, las terceras mayores/menores y las sextas mayores/menores.
- Disonantes: Intervalos que suenan tensos e inestables, creando un deseo de resolver en un intervalo consonante. Incluyen segundas, séptimas y todos los intervalos aumentados/disminuidos.
Los 12 intervalos básicos (dentro de una octava)
Aquí están los 12 intervalos fundamentales construidos sobre la nota Do, mostrados como intervalos armónicos. Se incluye un "ejemplo de canción famosa" para ayudarte a reconocerlos auditivamente.
1. Segunda menor (1 semitono)
Un intervalo muy disonante y tenso.
Ejemplo de canción famosa: El tema de "Tiburón".
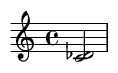
2. Segunda mayor (2 semitonos)
Un paso melódico común, menos áspero que una segunda menor.
Ejemplo de canción famosa: Las dos primeras notas de "Cumpleaños feliz".
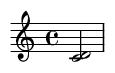
3. Tercera menor (3 semitonos)
Un intervalo consonante, a menudo descrito como triste o reflexivo.
Ejemplo de canción famosa: Las dos primeras notas de "Greensleeves".
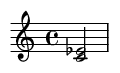
4. Tercera mayor (4 semitonos)
Un intervalo consonante, a menudo descrito como alegre o brillante.
Ejemplo de canción famosa: Las notas iniciales de "When the Saints Go Marching In".
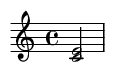
5. Cuarta justa (5 semitonos)
Un intervalo consonante estable y de sonido abierto.
Ejemplo de canción famosa: Las dos primeras notas de "La marcha nupcial" (Here Comes the Bride).
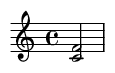
6. Tritono (6 semitonos)
El intervalo más disonante, también conocido como Cuarta Aumentada o Quinta Disminuida.
Ejemplo de canción famosa: Las notas iniciales de "Maria" de West Side Story.
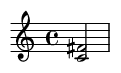
7. Quinta justa (7 semitonos)
Un intervalo muy fuerte, estable y consonante. La base de la armonía en la mayoría de las culturas.
Ejemplo de canción famosa: El tema principal de "La Guerra de las Galaxias".
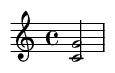
8. Sexta menor (8 semitonos)
Un intervalo consonante rico, que a menudo suena melancólico o romántico.
Ejemplo de canción famosa: Las dos primeras notas de "The Entertainer" de Scott Joplin.
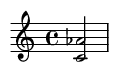
9. Sexta mayor (9 semitonos)
Un intervalo consonante brillante y claro.
Ejemplo de canción famosa: Las dos primeras notas de los tonos de NBC.
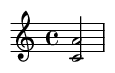
10. Séptima menor (10 semitonos)
Un intervalo disonante con un carácter "blues", central en el jazz y el rock.
Ejemplo de canción famosa: Las notas iniciales de "The Winner Takes It All" de ABBA.
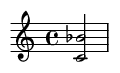
11. Séptima mayor (11 semitonos)
Una disonancia muy tensa, a menudo descrita como anhelante o conmovedora.
Ejemplo de canción famosa: Las dos primeras notas de "Take On Me" de A-ha (en el coro).
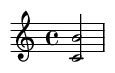
12. Octava (12 semitonos)
Perfectamente consonante. Es la misma nota, pero en un registro más agudo.
Ejemplo de canción famosa: Las dos primeras notas de "Over the Rainbow" de "El mago de Oz".
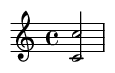
Más allá de la octava: Intervalos compuestos y extensiones de acordes
Los intervalos más grandes que una octava se llaman intervalos compuestos. Una novena mayor es simplemente una segunda mayor más una octava. En armonía moderna (especialmente jazz), estos intervalos se usan como "extensiones" o "tensiones" para añadir color y sofisticación a acordes básicos.
Aquí hay un acorde de Do Mayor 7 (Do-Mi-Sol-Si) con una Novena Mayor (Re) añadida en la parte superior para crear un acorde de Do Mayor 9.

Las extensiones comunes incluyen novenas, onceavas y treceavas, que pueden alterarse (por ejemplo, una novena menor o "bemol") para crear diferentes caracteres armónicos.
De los intervalos a las escalas y acordes
Las escalas y acordes no son colecciones aleatorias de notas; se construyen a partir de patrones precisos de intervalos.
Crear escalas con intervalos
Una escala es solo una secuencia de intervalos. Por ejemplo, la fórmula de la Escala Mayor es un patrón de tonos enteros (T, una Segunda Mayor) y semitonos (S, una Segunda Menor): T-T-S-T-T-T-S. Aplicar este patrón comenzando en Fa da la escala de Fa Mayor.
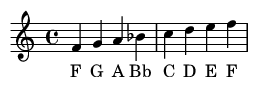
Crear acordes superponiendo intervalos
Los acordes se crean superponiendo intervalos sobre una nota fundamental, más comúnmente en terceras.
- Acorde Mayor: Fundamental + Tercera Mayor + Quinta Justa
- Acorde Menor: Fundamental + Tercera Menor + Quinta Justa
- Acorde Disminuido: Fundamental + Tercera Menor + Quinta Disminuida
- Acorde Aumentado: Fundamental + Tercera Mayor + Quinta Aumentada
A continuación se muestran estos cuatro tipos básicos de tríadas construidas sobre Fa.

Intervalos en progresiones armónicas
Las progresiones de acordes obtienen su sentido de movimiento y dirección de los intervalos entre las fundamentales de los acordes. El movimiento de fundamental más poderoso en la música tonal es una quinta justa descendente (o su inversa, una cuarta justa ascendente), que crea una fuerte sensación de llegada y resolución. La clásica progresión I-IV-V-I está impulsada por estas poderosas relaciones interválicas.

Figuras históricas:
Pitágoras (c. 570 – c. 495 a.C.): Mediante experimentos con un instrumento de una sola cuerda (monocordio), Pitágoras descubrió que los intervalos más consonantes (octava, quinta, cuarta) correspondían a proporciones numéricas simples (2:1, 3:2, 4:3). Esto sentó las bases para entender la música como una ciencia matemática.
Jean-Philippe Rameau (1683-1764): En su "Tratado de Armonía" (1722), Rameau propuso que la armonía no era arbitraria sino basada en la serie natural de armónicos. Estableció el concepto del "bajo fundamental", identificando la fundamental de los acordes y explicando cómo los intervalos crean tensión y res
