Summary:
The perfect fifth is arguably the most important musical interval after the octave. Spanning seven semitones, its pure, stable sound makes it the bedrock of harmony in Western music and beyond. From the overtones that give an instrument its color to the structure of chords and key relationships, the perfect fifth is an essential concept for any musician to understand.
Keywords:
perfect fifth, music theory, interval, consonance, harmony, overtone series, chord construction, circle of fifths, stability
Introduction: What is a Perfect Fifth?
Imagine the powerful opening of the "Star Wars" theme or the simple, familiar melody of "Twinkle, Twinkle, Little Star." The soaring, confident leap in both of those melodies is a perfect fifth. It's an interval that sounds strong, stable, and resolved. Its unique acoustic properties have made it the cornerstone of musical systems for centuries, from ancient Greek mathematical discoveries to the power chords of modern rock.
Definition and Characteristics
In music theory, an interval measures the distance between two pitches. A perfect fifth is an interval that encompasses seven semitones (or half steps). For example, on a piano, the distance from C to the G above it is a perfect fifth. You can find it by starting on any note and counting up seven keys, including both black and white keys.
Why "perfect"? The term refers to its high degree of consonance, or acoustic stability. This stability comes from its place in the natural overtone series. When a note is played on an acoustic instrument, it produces a fundamental frequency along with a series of quieter, higher-pitched overtones. The first overtone is the octave, and the second distinct overtone is a perfect fifth above that octave. This makes the perfect fifth (the 3rd harmonic) sound intrinsically related to the fundamental note, creating a pure and satisfying sound.
Examples in Notation
1. Melodic Perfect Fifths
A melodic interval occurs when two notes are played in sequence. Here are examples of ascending perfect fifths starting on different notes.
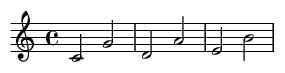
2. Harmonic Perfect Fifths and Triads
A harmonic interval occurs when two notes are played simultaneously. The perfect fifth forms the outer frame of all basic major and minor triads, providing their essential stability. The first measure shows a harmonic perfect fifth. The next two show how this interval is the backbone of both C Major and C minor chords.
The Exception: The Diminished Fifth (Tritone)
While most fifths in a major or minor scale are "perfect," there is one important exception. In any major scale, the fifth built on the seventh scale degree is a diminished fifth. This interval spans only six semitones instead of seven. For example, in the key of C Major, the interval from B (the 7th degree) to F is a diminished fifth. This dissonant, unstable interval is also known as a tritone, and its tension is crucial for creating harmonic movement and resolution in music.
Practical Applications and Ear Training
- Chord Construction: As shown above, perfect fifths are the stable outer shell of major and minor triads. They are also the basis of "power chords" (a root and a fifth) used extensively in rock and metal music for their strong, ambiguous sound (neither major nor minor).
- The Circle of Fifths: This fundamental music theory diagram organizes all 12 chromatic pitches in a sequence of perfect fifths. It's an essential tool for understanding key signatures, chord relationships, and modulation.
- Tuning: Instruments in the violin family (violin, viola, cello) are tuned in perfect fifths, making the interval physically integral to a string player's technique.
- Ear Training: To learn to recognize the perfect fifth by ear, use reference songs. The first two notes of "Twinkle, Twinkle, Little Star" (C-G) and the "Star Wars" main theme (G-D) are perfect fifths. Hum them to internalize the sound.
Historical Significance
Around 500 BCE, the Greek philosopher Pythagoras is said to have discovered the simple mathematical relationship of the perfect fifth, defining it by a frequency ratio of 3:2. This discovery laid the groundwork for Western tuning systems. Centuries later, composers like J.S. Bach mastered the use of fifth relationships to build the complex yet stable harmonic structures of the Baroque era. In the 20th century, composers like Paul Hindemith experimented with "quintal harmony," creating entire chordal systems by stacking fifths instead of the traditional thirds.
Fun Facts
The perfect fifth has a frequency ratio of 3:2, the simplest and most consonant ratio after the octave's 2:1. In traditional Chinese music theory, the five-note (pentatonic) scale can be generated by moving in a cycle of perfect fifths. The "open fifth" sound is so powerful that it's often used in film scores to evoke vastness, heroism, or ancient times.
Conclusion
The perfect fifth is more than just a theoretical concept; it's a fundamental building block of the music we hear every day. Its unique combination of mathematical purity and acoustic stability gives it a powerful, resolved sound that defines harmony, drives melody, and structures our entire system of keys. By learning to identify, understand, and use the perfect fifth, you gain a deeper insight into the very language of music.
References:
Christensen, T. (2002). The Cambridge History of Western Music Theory. Cambridge University Press.
Hindemith, P. (1942). The Craft of Musical Composition. Schott Music.
Lerdahl, F. (2001). Tonal Pitch Space. Oxford University Press.
