Musical Intervals: The Building Blocks of Music

Summary:

Musical intervals are the distances in pitch between any two notes, serving as the fundamental element upon which melody, harmony, and scales are constructed. A strong understanding of intervals is crucial for any musician, as they are the basic vocabulary of music. This article delves into their definition, classification, and application, providing clear examples and practical tips for recognizing them by ear.

Keywords:

Musical intervals, tones, semitones, consonance, dissonance, melody, harmony, ear training, music theory, scales, chords.

Introduction: What is a Musical Interval?

Imagine music is a language. If notes are the letters, then intervals are the syllables—the essential sounds that combine to form words (chords) and sentences (melodies). An interval is simply the distance between two pitches. This distance can be heard when notes are played one after the other (a melodic interval) or at the same time (a harmonic interval).

Mastering intervals transforms your relationship with music. It allows you to identify chords and melodies by ear, improvise with confidence, and understand the structure of any composition. It is the key that unlocks the door from simply playing notes to truly understanding the music you create and hear.

How to Define and Classify Intervals

Every interval has two parts to its name: a number (or distance) and a quality (or flavor).

1. Interval Number (Distance):

The number is found by counting the letter names from the first note to the second, including both. For example, the distance from C to G is a fifth because it spans five letter names: C, D, E, F, G.

• Unison: 1 letter name (C-C)
• Second: 2 letter names (C-D)
• Third: 3 letter names (C-E)
• Fourth: 4 letter names (C-F)
• Fifth: 5 letter names (C-G)
• Sixth: 6 letter names (C-A)
• Seventh: 7 letter names (C-B)
• Octave: 8 letter names (C-C)

2. Interval Quality (Flavor):

The quality describes the precise sound and size of the interval, measured in semitones (the smallest step in Western music, like from one piano key to the very next). Qualities are divided into two main families:

• Perfect: Unisons, fourths, fifths, and octaves are called 'Perfect'. They have a pure, stable sound.
• Major and Minor: Seconds, thirds, sixths, and sevenths can be 'Major' (larger) or 'Minor' (smaller). Major intervals often sound bright and happy, while minor intervals can sound more subdued or melancholic.

Additionally, any interval can be made a semitone larger (Augmented) or a semitone smaller (Diminished), which adds tension and color.

3. Acoustic Effect (Consonance vs. Dissonance):

Intervals can also be described by their sound:

• Consonant: Intervals that sound stable and at rest. Includes perfect intervals, major/minor thirds, and major/minor sixths.
• Dissonant: Intervals that sound tense and unstable, creating a desire to resolve to a consonant interval. Includes seconds, sevenths, and all augmented/diminished intervals.

The 12 Basic Intervals (Within an Octave)

Here are the 12 fundamental intervals built above the note C, shown as harmonic intervals. A "famous song example" is included to help you recognize them by ear!

1. Minor Second (1 semitone)

A very dissonant and tense interval.
Famous Song Example: The "Jaws" theme.

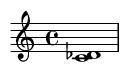
2. Major Second (2 semitones)

A common melodic step, less harsh than a minor second.
Famous Song Example: The first two notes of "Happy Birthday".

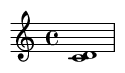
3. Minor Third (3 semitones)

A consonant interval, often described as sounding sad or pensive.
Famous Song Example: The first two notes of "Greensleeves".

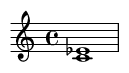
4. Major Third (4 semitones)

A consonant interval, often described as sounding happy or bright.
Famous Song Example: The opening notes of "When the Saints Go Marching In".

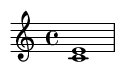
5. Perfect Fourth (5 semitones)

A stable, open-sounding consonant interval.
Famous Song Example: The first two notes of "Here Comes the Bride".

6. Tritone (6 semitones)

The most dissonant interval, also known as an Augmented Fourth or Diminished Fifth.
Famous Song Example: The opening notes of "Maria" from West Side Story.

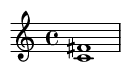
7. Perfect Fifth (7 semitones)

A very strong, stable, and consonant interval. The foundation of harmony in most cultures.
Famous Song Example: The "Star Wars" main theme.

8. Minor Sixth (8 semitones)

A rich consonant interval, often sounding plaintive or romantic.
Famous Song Example: The first two notes of "The Entertainer" by Scott Joplin.

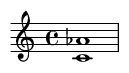
9. Major Sixth (9 semitones)

A bright, clear consonant interval.
Famous Song Example: The first two notes of the NBC chimes.

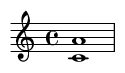
10. Minor Seventh (10 semitones)

A dissonant interval with a "bluesy" feel, central to jazz and rock.
Famous Song Example: The opening notes of "The Winner Takes It All" by ABBA.

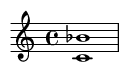
11. Major Seventh (11 semitones)

A very tense dissonance, often described as yearning or poignant.
Famous Song Example: The first two notes of "Take On Me" by A-ha (in the chorus).

12. Octave (12 semitones)

Perfectly consonant. It's the same note, but in a higher register.
Famous Song Example: The first two notes of "Somewhere Over the Rainbow".

Beyond the Octave: Compound Intervals and Chord Extensions

Intervals larger than an octave are called compound intervals. A major ninth is just a major second plus an octave. In modern harmony (especially jazz) , these intervals are used as "extensions" or "tensions" to add color and sophistication to basic chords.

Here's a C Major 7 chord (C-E-G-B) with a Major 9th (D) added on top to create a lush C Major 9 chord.

Common extensions include 9ths, 11ths, and 13ths, which can be altered (e.g., a minor or "flat" 9th) to create different harmonic flavors.

From Intervals to Scales and Chords

Scales and chords are not random collections of notes; they are built from precise patterns of intervals.

Creating Scales with Intervals

A scale is just a sequence of intervals. For example, the Major Scale formula is a pattern of whole steps (W, a Major 2nd) and half steps (H, a Minor 2nd): W-W-H-W-W-W-H. Applying this pattern starting on F gives you the F Major scale.

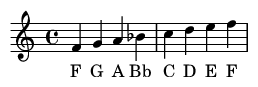
Creating Chords by Stacking Intervals

Chords are created by stacking intervals on top of a root note, most commonly in thirds.

• Major Chord: Root + Major Third + Perfect Fifth
• Minor Chord: Root + Minor Third + Perfect Fifth
• Diminished Chord: Root + Minor Third + Diminished Fifth
• Augmented Chord: Root + Major Third + Augmented Fifth

Below are these four basic triad types built on F.

Intervals in Harmonic Progressions

Chord progressions get their sense of movement and direction from the intervals between the roots of the chords. The most powerful root movement in tonal music is a descending perfect fifth (or its inverse, an ascending perfect fourth) , which creates a strong feeling of arrival and resolution. The classic I-IV-V-I progression is driven by these powerful interval relationships.

Historical Figures:

Pythagoras (c. 570 – c. 495 BC): Through experiments with a single-string instrument (monochord), Pythagoras discovered that the most consonant intervals (octave, fifth, fourth) corresponded to simple integer ratios (2:1, 3:2, 4:3). This laid the foundation for understanding music as a mathematical science.

Jean-Philippe Rameau (1683-1764): In his "Treatise on Harmony" (1722), Rameau proposed that harmony was not arbitrary but based on the natural overtone series. He established the concept of the "fundamental bass," identifying the root of chords and explaining how intervals create tension and resolution, which became the basis of modern tonal theory.

Paul Hindemith (1895-1963): In "The Craft of Musical Composition" (1937), Hindemith organized all 12 intervals into a hierarchical series based on their acoustic properties (consonance, dissonance, and tonal relationship to a root note), providing a systematic approach to analyzing both tonal and atonal music.

Interesting Facts:

• The tritone (augmented fourth/diminished fifth) was famously dubbed "diabolus in musica" (the devil in music) during the Middle Ages for its unsettling dissonance. Today, it is a cornerstone of blues, jazz, and metal.
• The phenomenon of octave equivalence—perceiving two notes an octave apart as the "same" note—is a cognitive universal found in almost every musical culture on Earth.
• Intervals carry strong emotional associations. Studies show that even non-musicians consistently link major thirds with happiness and minor thirds with sadness, suggesting a deep-seated human response to these sounds.
• Many musical traditions use microtones, which are intervals smaller than a semitone. For example, Arabic and Persian music employ "quarter-tones," which lie between the keys of a standard piano, creating unique melodic colors.

Conclusion: The Language of Music

Musical intervals are far more than a dry theoretical concept; they are the DNA of music. They shape melodies, build chords, and drive harmonic progressions. From the simple ratios discovered by Pythagoras to the complex tensions of modern jazz, intervals are the universal alphabet of musical expression.

For any developing musician, ear training for intervals is one of the most valuable skills you can build. Start by listening for the intervals in your favorite songs. Can you hear the perfect fifth in the Star Wars theme? Can you feel the tension of the minor second in the Jaws theme? By connecting the theory to the music you love, you will begin to understand the language of music on a profound new level.

References:

1. Kostka, S., Payne, D., & Almén, B. (2017). Tonal Harmony. McGraw-Hill Education.
2. Hindemith, P. (1942). The Craft of Musical Composition, Book I: Theory. Schott.
3. Levine, M. (1995). The Jazz Theory Book. Sher Music Co.
4. Tenney, J. (1988). A History of 'Consonance' and 'Dissonance'. Excelsior Music Publishing Company.
5. Meyer, L. B. (1956). Emotion and Meaning in Music. University of Chicago Press.